Mathematics Education: A Way Forward

Population × Bad curriculum ^{Multiple generations} = Functionally innumerate population

The objective of good math teaching should not be to "cover the curriculum" but to show students how to explore our fascinating and beautiful world through the lens of mathematics. We must change our focus in math education from a focus on a largely irrelevant and uninteresting set of learning objectives to a focus on making math relevant and engaging for students.

What's wrong with this picture?

Start by checking out this graphic from the Canadian Council on Learning.

Statistics Canada defines numeracy as "[t]he knowledge and skills required to effectively manage the mathematical demands of diverse situations." It is clear from the CCL diagram that we are failing miserably!

I believe this is because of the way we teach mathematics as a series of computations rather than a tool for solving open ended and interesting problems. Specifically we spend far too little time in mathematics education giving students opportunities to learn problem solving and pattern finding. More importantly, too little of the mathematics we learn is situated in a useful context for students and as a result our mathematics curriculum is unmotivated in the eyes of the people learning it. As high school math teacher Dan Meyer said in his TED talk , “I sell a product to a market that doesn't want it, but is forced by law to buy it.”

In his essay “A Mathematician’s Lament” Paul Lockhart says,

“I don’t see how it’s doing society any good to have its members walking around with vague memories of algebraic formulas and geometric diagrams, and clear memories of hating them.”

We have many people who have learned school math, but don't apply it to their lives and hated learning it. Why do we think this is useful?

The importance of relevance in teaching mathematics cannot be over-stated. How often are mathematics teachers asked “Why are we learning this?” The reasons “you will use this in college”, “it is going to be on the test” or “this is useful in engineering” are not relevant to most K to 12 students. Therefore many students disengage from learning mathematics because of unsatisfactory answers to their reasonable question, and we end up using methods of coercion to force them into learning an unsatisfying curriculum.

For further reading on this issue, I strongly recommend The Four Pillars Upon Which the Failure of Math Education Rests by Matthew A. Brenner.

A New Frame

One immediate place we can make a change is to start by re-examining the structure of the curriculum. Currently, we have a structure where mathematical computations are at the centre of the curriculum.

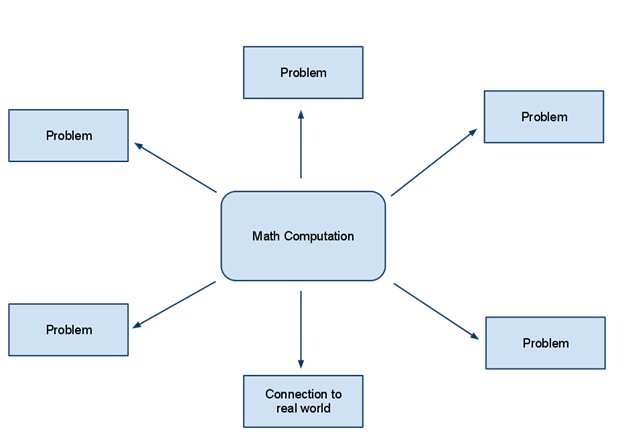
Here the context of mathematics is added, almost as an afterthought, often in the form of poorly designed word problems contained in textbooks. As a textbook writer myself, I know the inherent difficulties in designing these problems, and the impact the focus on computational structure has on the decisions that are made behind the scenes.

I propose a structure for constructing mathematics curriculum to ensure that it is relevant. Instead of computations at the centre of the curriculum, let’s put the relevancy or the “real world” at the centre.

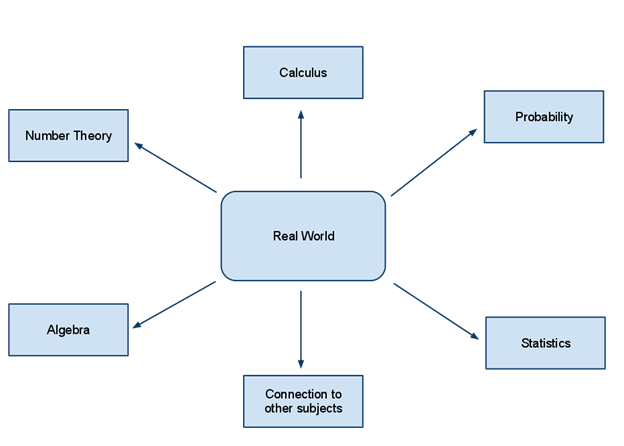
The world is full of mathematics which is interesting. The forms of trees are the result of fractal branching patterns. A small snail shell spirals in a sophisticated and beautiful mathematical pattern. Deep mathematics resides in the large-scale structure of the universe. Everything we look at has a mathematical structure.

Simple Ideas for Making Mathematics Relevant

Here are few suggestions so you can begin to make the transition to a real-world centered curriculum. If you have other ideas, please add them in the comments below.

• Photos of mathematical ideas require a bit of work and creativity to make useful, but the newspaper is full of examples of mathematics in context.
   
• Grocery flyers provide ample opportunities to practice percents.
   
• Instead of a worksheet on adding change, give students actual change to count or have them work in the school store.
   
• Cooking involves proportions and fractions.
   
• Determining whether (or not) your catapult will hit the target involves trigonometry and quadratic functions.

Join this Math in the Real World Flickr group to find and share more ideas. Check out the #realmath hashtag on Twitter where math teachers are sharing other ideas regularly.

Resources for Boosting Engagement

While relevant mathematics is an important part of the restructuring, it is not the only mathematics I would teach. There are thousands of mathematical ideas which lack meaningful relevance to the world but which are highly engaging.

Problem solving

• Use problems like the Bridges of Königsberg problem to help students develop mathematical patience and learn how to overcome frustration. As an added bonus, your students will learn that not all problems have solutions.
   
• Gordon Hamilton, of Math Pickle, suggests another approach. He has created activities which allow students to explore difficult mathematical problems and learn that mathematics is an activity in which we experiment and explore ideas.
   
• Project Euler describes itself as "a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve."

Technology

• Simulations and interactive diagrams make understanding difficult concepts in mathematics a lot easier. I've found the Mathematics Visualization Toolkit distributed by the University of Colorado to be exceptionally useful in sharing complex diagrams with students. The Wolfram Alpha demonstrations project includes thousands of useful online models for math and science. Check out this interactive diagram here, created using Geogebra.
  
  
  Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)
• Multimedia is a drastically under-utilized resource in most mathematics classrooms. I've had students create their own videos to explain their solutions, explain a concept, describe a problem, and even replace traditional word problems. Look at this example of a student explaining lines of best fit.
  
  

  
   

• For hundreds of other examples of kids explaining concepts via video, check out MathTrain.TV, a tutorial resource built by 6th grade students.
   
• The Computer Based Math project is "a project to build a completely new math curriculum with computer-based computation at its heart—alongside a campaign to refocus math education away from historical hand-calculating techniques and toward relevant and conceptually interesting topics."
   
• Even traditional practice exercises can often be turned into more interesting problems. One popular activity with students is to draw something, for example a robot, and then determine how to create their drawing with mathematical functions.

One time a student created a graph requiring 187 different equations of lines. When I asked him why he did so much work, he responded, "I really liked my robot, and I wasn't willing to change it just because it was more work." I'd really like to hear this more often from students, wouldn't you?